Zero-Knowledge Proof Vulnerability Analysis and Security Auditing

Abstract: Zero-Knowledge Proof (ZKP) technology marks a revolutionary advancement in the field of cryptography, enabling the verification of certain information ownership without revealing any specific details. This technology, with its paradoxical yet powerful characteristics, provides a solid foundation for a wide range of applications, especially in enhancing the privacy and security of blockchain technology and other cryptographic systems. As ZKP technology increasingly becomes a part of the blockchain infrastructure, its importance for security and completeness becomes more pronounced. However, the complexity of ZKP implementation and the rapid iteration of the technology introduce various vulnerabilities, challenging the privacy and security it aims to offer.

This study focuses on the completeness, soundness, and zero-knowledge properties of ZKP to meticulously classify existing vulnerabilities and explores multiple categories of vulnerabilities, including completeness issues, soundness problems, information leakage, and non-standardized cryptographic implementations. Furthermore, we propose a set of defense strategies that include a rigorous security audit process and a robust distributed network security ecosystem. This audit strategy employs a divide-and-conquer approach, segmenting the project into different levels, from the application layer to the platform-nature infrastructure layer, using threat modelling, line-by-line audit, and internal cross-review, among other means, aimed at comprehensively identifying vulnerabilities in ZKP circuits, revealing design flaws in ZKP applications, and accurately identifying inaccuracies in the integration process of ZKP primitives.

Keywords: Zero-Knowledge Proofs (ZKP) · Cryptographic Security · Vulnerability Analysis · Defense Mechanisms · Audit Tools and Methodologies.

1 Introduction

ZKP is a cryptographic protocol that allows a prover to demonstrate the truth of a statement to a verifier without revealing any additional information beyond the validity of the statement itself. This unique attribute makes ZKP a powerful tool for enhancing privacy and security across various applications[1–9].

The applications of ZKP are wide-ranging and influential[10]. In blockchain technology, ZKP is used to protect the privacy of transactions while ensuring the completeness of the ledger. Moreover, it finds application in identity verification processes[11], allowing for the authentication of individual credentials without disclosing specific information[12]. Other use cases for ZKP include privacypreserving voting systems, verifying the validity of rollups on the base Layer 1, and compressing blockchain states[13].

By exploring the background and key concepts of ZKP, we can appreciate its significance and the diversity of its applications. Nevertheless, the complexity of ZKP implementations introduces a variety of vulnerabilities[14–16]. The following sections of this paper will delve into these vulnerabilities and explore the ongoing necessity for their analysis and audit. This is crucial for maximizing the potential of ZKP and ensuring the privacy[17] and security[18] it aims to provide.

2 Vulnerabilities in ZKP

The unique properties of ZKP have become the cornerstone for maintaining privacy in various cryptographic applications, fundamentally relying on its three main attributes: completeness, soundness, and the zero-knowledge aspect. Completeness ensures that true statements can be reliably proven; soundness guarantees that false statements are not mistakenly recognized as true[19–22]; and the most crucial, the zero-knowledge property, ensures that no additional information beyond the truthfulness of the statement is revealed during the proof process. These attributes together make ZKP a key tool for facilitating secure and confidential digital interactions, especially in blockchain technology, where they achieve a balance between transparency and confidentiality.

However, the characteristics of ZKP also mean it often plays a critical role in key aspects of applications, such as protecting user privacy or verifying crucial proofs of financial assets. If any vulnerabilities exist and are maliciously exploited, this could severely threaten the privacy and security protections ZKP aims to provide. In the context of blockchain, these vulnerabilities not only threaten the network’s completeness and security but can also lead to direct financial losses and undermine trust in decentralized systems. Addressing these vulnerabilities requires a deep understanding of ZKP’s theoretical framework and practical applications, a task made particularly complex by the sophisticated mathematical structures underlying ZKP. This complexity highlights the necessity for ongoing and careful scrutiny and effective mitigation strategies to prevent potential security vulnerabilities[23]. Therefore, to facilitate a more systematic analysis, this study classifies the vulnerabilities in ZKP based on the three core attributes of zero-knowledge proofs.

2.1 Completeness Issues

Over-constrained Circuits.

Over-constrained circuits refer to the addition of extra constraints on a circuit that is already normally constrained, leading to the circuit’s inability to successfully prove or verify. This issue may stem from the mechanisms of the compilers themselves. Taking circom and halo2 as examples, they establish constraints through assertions while compiling circuits. However, during the optimization process of compiling circuits, the compiler might introduce additional assertions, causing the inputs and outputs not to satisfy the constraints at the time of proving, thereby leading to errors. Additionally, developers adding too many or redundant constraints when designing circuits could also trigger such issues.

In the early versions of the Poseidon hash circuit within Scroll’s zkEVM, there is a section of code that uses the variable mpt_only to control the hash processing mode. In this circuit, specific lines start in a custom way and are subject to zero-padding restrictions. When mpt_only = true, it means there is one custom line and two field elements need to be hashed; conversely, it implies there are two custom lines. This represents the variability in the length of variable inputs.

config.s_custom.enable(region, 1)?;
if self.mpt_only {
  return Ok(1);
}

Based on the return value in the code, when self.mpt_only is set to true, the circuit erroneously marks the second line as custom. This means that the line, which should have been used for hash input, is now overly constrained to zero.

Therefore, any attempt to hash with non-zero input will fail because the excessive constraint on the second line contradicts its original design purpose, conflicting with its intended function to accommodate hash inputs.

2.2 Soundness Issues

Under-constrained Circuits.

The vulnerabilities related to under-constrained circuits refer to instances during the design or programming implementation of circuits where certain constraints are either not set or incompletely set. This can result in the circuit exhibiting uncertain behavior or producing unintended results. In specific cases, such under-constrained circuits can lead to serious consequences. For instance, in the incremental merkle tree implemented by the ZK-kit smart contracts, there’s a lack of range constraints on the values of leaf nodes, which allows malicious attackers to exploit this vulnerability to generate illegitimate zero-knowledge proofs, thereby facilitating the repeated extraction of funds.

A typical example can be found in "Missing Bit Length Check" in Dark Forest v0.3:

template RangeProof(bits, max_abs_value) {
  signal input in;
  component lowerBound = LessThan(bits);
  component upperBound = LessThan(bits);
  ...
}

In this version, the RangeProof template implemented by Dark Forest directly invokes the LessThan template from the circomlib library to compare the size of input data. However, LessThan does not set actual constraints on the bit length of the input data, resulting in the inability to limit the bit length of inputs via the max_abs_value parameter when calling RangeProof. Consequently, attackers can input a max_abs_value and an in value that exceed the expected maximum number of bits, thus constructing a legitimate proof that can pass the RangeProof verification.

• Nondeterministic Circuits.

Nondeterministic circuits vulnerabilities are a type of under-constrained circuits vulnerability, specifically referring to those situations where the lack of explicit constraints allows the circuit to produce multiple valid proofs for the same output. For example, in the Tornado Cash system, to prevent the double-spending of the same Note, users need to generate and reveal a nullifier when spending a note commitment. If a user attempts to use the same Note commitment a second time, they must reveal the same nullifier, an action that would be revoked by the smart contract. However, if the zeroknowledge proof circuit has nondeterministic vulnerabilities, malicious attackers could exploit this for double-spending attacks.

In the vulnerability "Circom-Pairing, Missing Output Check Constraint", the Circom-Pairing circuit, when dealing with integers that require the use of more than 254-bit prime fields, calls the Circom big-int library. To ensure the accuracy of the computations, the Circom-Pairing circuit would typically use the BigLessThan circuit to ensure all numbers are less than a certain upper limit.

template CoreVerifyPubkeyG1(n, k) {
  ...
  var q[50] = get_BLS12_381_prime(n, k);
  component lt[10];
  // check all k input arrays are correctly
  // formatted bigints < q
  // BigLessThan calls Num2Bits
  for(var i=0; i<10; i++) {
    lt[i] = BigLessThan(n, k);
    for(var idx=0; idx<k; idx++) {
      lt[i].b[idx] <== q[idx];
    }
  }
  for(var idx=0; idx<k; idx++) {
    lt[0].a[idx] <== pubkey[0][idx];
    lt[1].a[idx] <== pubkey[1][idx];
  }
}

In the CoreVerifyPubkeyG1 circuit, although BigLessThan was called multiple times to ensure pubkey < q, there were no constraints on the output of BigLessThan. This resulted in proofs where pubkey >= q and BigLessThan correctly outputted a result still being successfully verified and accepted.

• Mismatching Bit Lengths.

The mismatching bit lengths vulnerability refers to the failure to properly constrain the bit length of signals within a circuit, leading to circuit outputs that are inconsistent with expectations. This type of vulnerability is a common form of under-constrained circuits vulnerability, particularly noticeable when building circuits with circom.

Attackers can deliberately provide input parameters with mismatching bit lengths to bypass preset verification restrictions or compromise system security, thereby causing information leakage, verification errors, or other forms of security issues. Specifically, when the bit length of input parameters does not match what the circuit expects, the verification process may fail. In such cases, zeroknowledge proofs may become ineffective, preventing the system from accurately verifying the required evidence and posing a serious threat to the security and reliability of the entire protocol.

Take, for example, the LessThan circuit in circomlib. It accepts two input parameters, in[0] and in[1], and uses the parameter n to limit the maximum bit length of the inputs. If in[0] < in[1], LessThan outputs 1; otherwise, it outputs 0.

template LessThan(n) {
  assert(n <= 252);
  signal input in[2];
  signal output out;
  component n2b = Num2Bits(n+1);
  n2b.in <== in[0]+ (1«n) - in[1];
  out <== 1-n2b.out[n];
}

LessThan calls the Num2Bits circuit to convert the inputs to bit form but does not set specific constraints on the bit length of the input to Num2Bits. As a result, the circuit effectively compares the lower n bits of in[0] to in[1]. Therefore, even if the length of in[0] exceeds n and is greater than in[1], LessThan might still output 1.

• Unused Public Inputs Optimized Out.

In Circom 1.0, there was a scenario where many circuits introduced a variable as a public input without imposing any constraints on it. These unconstrained public inputs could serve as critical information during the proof verification. However, in the compiler for Circom 2.0, if these public inputs are found to be irrelevant to any constraints, the optimizer will remove them from the circuit.

When public inputs of a circuit are used for data storage or transmission and are removed due to the intervention of the optimizer, it may lead to data loss, causing errors in program logic or issues with data completeness. More seriously, if the public inputs in a circuit are not properly constrained, malicious attackers could exploit this vulnerability to forge proofs, threatening the security of zero-knowledge proof applications.

Take the zero-knowledge proof application Semaphore as an example, which allows users to send messages while remaining anonymous. Semaphore hashes the messages sent by users and then uses the resulting hash value as one of the public inputs for the proof.

template Message(){
  signal input message_plaintext;
  signal input message_hash; // public
  ...
}

According to the example code, if Semaphore’s developers do not set any constraints on these variables, malicious attackers could tamper with the user information hash value in the public inputs to obtain a valid proof. Proofs modified in this way could be used for replay attacks, allowing attackers to forge any message.

• Assigned but not Constrained.

In Circom and halo2, the assignment and constraint of signals within a circuit are designed to be conducted separately, aiming to provide developers with a convenient means of signal assignment. However, in practice, many circuits neglect to apply the necessary constraints after completing signal assignment, leading to the emergence of the "Assigned but not Constrained" vulnerability.

When this type of vulnerability exists in the source code of circom and halo2, malicious attackers could fork the source code and then modify the values of related assignment expressions. This alteration could change the values of other signals to bypass the circuit’s constraints, forging a legitimate proof.

Take the IsZero circuit in circomlib as an example. This circuit determines if input in is equal to 0 by checking if the inverse inv of in exists.

template IsZero() {
  signal input in;
  signal output out;
  signal inv;
  inv <– in!=0 ? 1/in : 0;
  out <== -in*inv +1;
  in*out === 0;
}

Due to Circom’s syntax limitations, it’s not possible to directly use constraints to determine whether the inverse (inv) of in exists. Therefore, it is necessary first to calculate the inv of in through an assignment, then use it to construct constraints on in and out to determine if in is 0.

Similarly, in the PSE zkEVM using halo2, for the handling of the SHL and SHR opcode circuits, although the following code correctly assigns values to inputs shf0 and shift, it lacks the necessary constraint to force shf0 to be set to the first byte of shift.

let shf0 = pop1.to_le_bytes()[0];
...
self.shift.assign(region, offset, Some(pop1.to_le_bytes()))?;
self.shf0.assign(region, offset, Value::known(u64::from(shf0).into()))?;

2.3 Information Leakage

Trusted Setup Leak.

Trusted Setup Leak refers to the issue in cryptographic protocols based on zero-knowledge proofs where the parameter generation process might expose sensitive information, thereby compromising the security of the protocol. If any participant involved in generating the parameters retains some secret values, they could potentially use this information to forge valid proofs, deceiving other participants or stealing their assets.

Take Zcash as an example, a cryptocurrency that relies on zk-SNARKs technology to protect user privacy. The implementation of zk-SNARKs requires a trusted setup process to generate crucial parameters, and the confidentiality of these parameters is essential; otherwise, attackers could exploit them to forge valid proofs. Although there are concerns that parameters might be leaked during Zcash’s trusted setup process, giving attackers an opportunity, there have been no reports to date of this vulnerability being successfully exploited for attacks.

2.4 Arithmetic Over/Under Flows

In the field of zero-knowledge cryptography, modular arithmetic operations are common, typically performed over scalar fields. However, due to the limitations of finite field orders, failing to properly handle arithmetic overflows and underflows can lead to issues. For example, in Circom, all integers are established on a scalar field with the following order:

p=21888242871839275222246405745257275088548364400416034343698204186575808495617

In zero-knowledge proof applications built using circom, ignoring the order of the field or not correctly handling overflows and underflows can result in certain constraint statements producing incorrect results, such as:

(0-1)===21888242871839275222246405745257275088548364400416034343698204186575808495616;

(21888242871839275222246405745257275088548364400416034343698204186575808495616+1)===0;

If arithmetic overflows and underflows are not properly handled, this may cause errors in the verification process or be exploited by malicious attackers to bypass intended verification restrictions.

A typical "Missing Smart Contract Range Check" vulnerability was discovered in the Semaphore application. Semaphore is a decentralized application built on Ethereum that allows users to prove they are members of a group using zero-knowledge proofs without revealing their specific identity. Given that Solidity’s uint256 type can contain values exceeding the SNARK scalar field, Semaphore stipulates that if an input group ID exceeds the order of the SNARK scalar field, the smart contract’s verification will fail. The logic code is as follows:

require(input[i] < snark_scalar_field, "verifier-gte-snark-scalar-field");

However, when a new group is created, any valid uint256 type number can be input as the group ID, leading to a scenario where if the group ID exceeds the range of the SNARK scalar field at creation, the group member’s identity verification will never pass.

Therefore, to ensure the reliability and security of zero-knowledge proof applications, it is crucial to thoroughly consider and address arithmetic overflows and underflows during design and implementation, to prevent related vulnerabilities.

2.5 Unstandardized cryptographic implementation

Forging of Zero Knowledge Proofs.

If a zero-knowledge proof protocol has security flaws, then a malicious prover could construct forged proofs that pass verification. These forged proofs can be used to "prove" any claim the prover wishes to assert, a type of security vulnerability that the TrailOfBits team has dubbed the "Frozen Heart" vulnerability.

The "Frozen Heart" vulnerability is a serious security flaw that can compromise the correctness of various zero-knowledge proof systems, including PlonK and Bulletproofs. Once a zero-knowledge proof system is affected by such a vulnerability, safeguards for user privacy, data completeness, and transaction security, among others, can become ineffective.

Many zero-knowledge proof protocols adopt the Fiat-Shamir transformation for non-interactive verification, which fundamentally relies on the so-called “random oracle model.” However, as TrailOfBits points out, the implementation of the Fiat-Shamir transformation generally faces execution issues, mainly due to a lack of specific guidance for different protocol implementations. Typically, the design papers of protocols do not include all the critical details needed in coding practices in detail, leading to flaws and vulnerabilities during implementation. These vulnerabilities provide attackers with opportunities to successfully forge proofs, thereby undermining the correctness and security of zero-knowledge proof systems. To address this challenge, TrailOfBits recommends providing more detailed implementation guidance to assist developers in accurately implementing the Fiat-Shamir transformation, thereby avoiding potential security risks.

Bad Randomness.

The essence of zero-knowledge proofs lies in the ability to verify a party’s knowledge or attributes without revealing any additional information, where randomness plays a crucial role. Once a protocol employs an inappropriate source of randomness, it may allow attackers to predict or infer the generated random numbers, rendering the interaction between the prover and verifier meaningless. If the proof system used by the prover has defects in randomness, then sensitive information may be leaked. Similarly, if the random challenges issued by the verifier are singular or predictable, attackers could prepare false proofs in advance to deceive the verifier.

Take the Schnorr signature scheme as an example, a signing mechanism based on the Discrete Logarithm Problem, often used as an example of interactive and non-interactive zero-knowledge proofs. In this scheme, the prover needs to choose random blinding factors to generate a proof or signature.

fn schnorr_sign(message: &[u8], private_key: &[u8]) -> ([u8; 32], [u8; 32]) {
  let k = generate_random(); // Secure random blinding factor
  // or not secure
  let r = calculate_r(&k); // Depends on k
  let s = calculate_s(&r, message, private_key); // Signature
  // calculation
  (r, s);
}

According to the pseudocode above, if the blinding factors used by the prover in generating a signature can be predicted by attackers, or if the same blinding factors are reused across multiple signing operations, or if the blinding factors for one signature are arithmetically operated on or transformed to obtain the blinding factors for the next signature, it could lead to the leakage of secret information. Even if only a few bits of the blinding factors are leaked, attackers might deduce the complete blinding factors through guessing and brute-force methods, thereby revealing sensitive information.

Bad Polynomial Implementation.

"Bad Polynomial Implementation" involves implementation flaws in the polynomial computation process of zeroknowledge proof protocols, which might stem from programming errors, poor algorithm choices, or a lack of understanding of mathematical properties. These issues can occur in critical components of zero-knowledge proof protocols, such as constructing polynomial commitments, performing polynomial evaluations, or verifying polynomial equations. Improper handling of polynomials may lead to inaccurate computational results or leak information that should remain confidential, thereby compromising the security and effectiveness of zero-knowledge proofs.

Zendoo, a protocol that utilizes zero-knowledge proofs for cross-chain transfers, implements methods for handling dense polynomials for Fast Fourier Transform (FFT) in its fft/polynomial/dense.rs file. When using the add() function to perform addition on two polynomials of the same degree, if the sum of the trailing coefficients is zero, these coefficients are not trimmed. This results in the leading term of the generated polynomial having a non-zero coefficient, contradicting the fundamental principles of polynomial representation.

fn add(self, other: &’a DensePolynomial<F>) -> DensePolynomial<F> {
  if self.is_zero() {
    other.clone()
  } else if other.is_zero() {
    self.clone()
  } else {
    if self.degree() >= other.degree() {
      let mut result = self.clone();
      for (a, b) in result.coeffs.iter_mut().zip(&other.coeffs) {
        *a += b
      }
      result
    } else {
      let mut result = other.clone();
      for (a, b) in result.coeffs.iter_mut().zip(&self.coeffs) {
        *a += b
      }
      // If the leading coefficient ends up being zero, pop it off.
      while result.coeffs.last().unwrap().is_zero() {
        result.coeffs.pop();
      }
      result
    }
  }
}

For example, performing addition on two polynomials with coefficients [3, 2, 1] and [1, 0, p-1] through the above code would result in coefficients [4, 2, 0], where the trailing zero coefficient is not trimmed. Although the else branch of the add() function performs a trimming operation, failure to correctly handle this in all cases could cause panic when calling the degree() function below, leading to erroneous calculations or denial-of-service attacks.

// Returns the degree of the polynomial.
pub fn degree(&self) -> usize {
  if self.is_zero() {
    0
  } else {
    assert!(self.coeffs.last().map_or(false, |coeff| !coeff.is_zero()));
    self.coeffs.len() - 1;
  }
}

Deprecated Hash Function.

The security and effectiveness of ZKP depend on the correct implementation and security of its cryptographic primitives, such as hash functions. With the increase in computing power, some early hash functions, such as MD5, SHA-1, RIPEMD, RIPEMD-128, and Whirlpool, are no longer considered secure.

Using these deprecated hash functions could make it easier for attackers to predict or reveal confidential information through brute force attacks, thereby undermining the fundamental properties of zero-knowledge proofs.

For example, in Tornado Cash, the following circuit shows how a user can generate a note using a secure hash function to be able to withdraw stored ETH in the future.

// computes Pedersen(nullifier + secret)
template CommitmentHasher() {
  signal input nullifier;
  signal input secret;
  signal output commitment;
  signal output nullifierHash;
  component commitmentHasher = Pedersen(496);
  component nullifierHasher = Pedersen(248);
  component nullifierBits = Num2Bits(248);
  component secretBits = Num2Bits(248);
  nullifierBits.in <== nullifier;
  secretBits.in <== secret;
  for (var i = 0; i < 248; i++) {
    nullifierHasher.in[i] <== nullifierBits.out[i];
    commitmentHasher.in[i] <== nullifierBits.out[i];
    commitmentHasher.in[i + 248] <== secretBits.out[i];
  }
  commitment <== commitmentHasher.out[0];
  nullifierHash <== nullifierHasher.out[0];
}

If this circuit used an insecure hash function, such as MD5 or SHA-1, to construct the user’s note, attackers might attempt to create hash collisions and generate new proofs to withdraw the user’s stored ETH, achieving theft.

Therefore, when constructing zero-knowledge proof circuits or proof systems, it is advisable to prioritize secure hash functions. For example, the Pedersen hash function, widely used in some ZK frameworks like halo2, or other zk-friendly hash functions such as Poseidon, MiMC, etc.

3 Case Study

3.1 Soundness Vulnerability in zkSync Era Mainnet

zkSync Era is an innovative Layer 2 scaling solution designed to address the scalability challenges of the Ethereum while maintaining its security and decentralization principles[24]. Within zkSync Era’s virtual machine (EraVM), the execution of write instructions relies on two special structs, MemoryWriteQuery and RawMemoryQuery.

The value to be written is initially stored in the MemoryWriteQuery struct as two registers, then split into three values: lowest_128, u64_word_2, and u64_word_3. These values are constrained through LinearCombination to ensure the correctness of the splitting process. Ultimately, these values are packaged and stored in RawMemoryQuery. However, the vulnerability exists within the code for applying linear constraints:

let mut lc = LinearCombination::zero();
lc.add_assign_number_with_coeff(&u64_word_2.inner, shifts[0]);
lc.add_assign_number_with_coeff(&u64_word_3.inner, shifts[64]);
lc.add_assign_number_with_coeff(&highest_128.inner, minus_one);

This code snippet is intended to constrain the value of lc to 0, but it fails to call lc.enforce_zero(cs) or lc.into_num(cs) to actually apply the constraint. This leads to the highest 128 bits in MemoryWriteQuery being unconstrained, allowing malicious provers to replace these 128 bits with any value, generating a fake proof that would be accepted.

Attack plans and strategies exploiting the vulnerability:

This vulnerability allows the prover to modify the highest 128 bits of the value stored in memory and generate a valid proof. There are various ways to exploit this vulnerability, where attacking the L2EthToken system contract is a relatively easy method.

According to the zkSync Era mechanism, transactions withdrawing ETH from zkSync Era to the mainnet first send verification information to L1, followed by creating two MemoryWriteQuery objects to record the withdrawal amount parameter _amount. Therefore, malicious attackers can exploit this mechanism by modifying the code that handles the write operation to perform the following actions:

• Check if the _amount value being written matches a specific value, such as 0x1371337137 or 0.00002 ETH.

• If it matches, modify the high 128 bits of the written value, turning _amount into a huge value, for example, 0x152d0000133713371337 or ˜100K ETH.

Through the above operations, when a malicious attacker initiates a transaction withdrawing ETH from zkSync Era to the mainnet, the value of _amount will be adjusted to a figure far exceeding the actual withdrawal amount, allowing the attacker to successfully steal a large amount of ETH.

3.2 Vulnerability in MACI

The Minimal Anti-Collusion Infrastructure (MACI) is an open-source public platform designed to provide a confidential on-chain voting mechanism[25]. In the MACI protocol, two types of messages are distinguished: vote/key change messages and top-up messages. The message type is identified by its first index in an array (msgs[0]), where 1 represents a vote/key change message, and 2 represents a top-up message. Users can publish their messages through the publishMessage() function within poll.sol, using their own parameters. If users intend to post a top-up message to increase their voting balance, they need to use the topup() function, which first attempts to retrieve the user’s new top-up amount. If retrieval fails, the user cannot submit a top-up message.

However, in the MACI implementation, there is a lack of sufficient validation and constraint on the message type within the publishMessage() function. This oversight allows malicious attackers to arbitrarily modify the message type, thereby executing unauthorized operations.

function publishMessage(Message calldata _message, PubKey calldata _encPubKey)
public
isWithinVotingDeadline {
  // we check that we do not exceed the max number of messages
  if (numMessages == maxValues.maxMessages) {
    revert TooManyMessages();
  }
  // validate that the public key is valid
  if (_encPubKey.x >= SNARK_SCALAR_FIELD || _encPubKey.y >= SNARK_SCALAR_FIELD) {
    revert MaciPubKeyLargerThanSnarkFieldSize();
  }
  // cannot realistically overflow
  unchecked {
    numMessages++;
  }
  // need to restrict the msgType to 1: message.msgType = 1
  uint256 messageLeaf = hashMessageAndEncPubKey(_message, _encPubKey);
  extContracts.messageAq.enqueue(messageLeaf);
  emit PublishMessage(_message, _encPubKey);
}

Attack plans and strategies exploiting the vulnerability:

In the implementation of MACI, it was originally designed that users could only top up their accounts if they had actual on-chain credit, to ensure the fairness of the voting system. However, due to the lack of sufficient verification and constraints on message types in the publishMessage() function, malicious users were able to modify the message type to 2, erroneously triggering the system to recognize it as a top-up message. This oversight allowed users without actual on-chain credit to falsely top up their accounts, thereby illegitimately gaining increased voting balances. Such actions could ultimately enable attackers to obtain voting rights far beyond reasonable limits, undermining the fairness and effectiveness of the entire voting mechanism.

4 Vulnerability Defense Strategies

The root cause of these vulnerabilities lies in circuits not being fully constrained. Although these vulnerabilities have not led to severe consequences in the current security environment, the advancement of distributed network technology is gradually diminishing the development teams’ direct control over protocols. This trend significantly increases the potential risk of malicious attackers submitting attack code, making it especially crucial to formulate appropriate security strategies to counter such threats.

Firstly, during the circuit design phase, rigorous mathematical forms, such as R1CS or QAP, should be used to precisely describe the circuits to be implemented. This practice helps check for unconstrained conditions after the circuit’s concrete implementation. Moreover, after the circuit implementation, it is essential to carefully verify that each variable in the circuit is constrained by its bit length and to test with inputs that exceed the prime field range of the circuit, effectively eliminating potential vulnerabilities of arithmetic overflow. Ultimately, it requires considering the overall project perspective to check if other modules may affect the security of ZKP. For example, reviewing the uint256 data type variables used directly for zero-knowledge circuit computations in smart contracts to ensure there are no mismatches in bit length.

Regarding the issue of needing a trusted setup in zk-SNARKs[26–28], secure multiparty computation techniques can be utilized, allowing multiple participants to jointly contribute randomness to generate a Common Reference String (CRS). As long as at least one participant destroys their private entropy part, the security of the CRS can be ensured. Additionally, consider adopting zero-knowledge proof protocols that do not require a trusted setup, such as zkSTARK and halo2, to fundamentally eliminate potential security risks during the zk-SNARK initialization process.

4.1 Conducting Security Audits for ZKP

Zero-Knowledge Proof technology plays a crucial role in multiple domains such as blockchain, authentication, voting systems, the Internet of Things, and more. Despite its significance, it also faces challenges in complex computations and validations. To ensure the correctness and security of ZKP applications, conducting security audits is an indispensable step. Security auditing of ZKP applications is not only a key task but also a process that helps developers and users identify potential vulnerabilities and errors, thereby enhancing the application’s trustworthiness and security level.

There are various security auditing methods, including static analysis, dynamic testing, and manual verification, each with its advantages, disadvantages, and applicable scenarios. During the security audit process, it is necessary to consider multiple factors such as the program’s scale, complexity, security requirements, performance demands, and cost-effectiveness[29–32].

With the advancement of ZKP technology and the expansion of its application scope, the importance of security audits is increasingly recognized, presenting greater challenges. Therefore, continuously innovating and improving audit strategies and tools to ensure the correct execution and security of applications is an inevitable trend for future development.

4.2 Audit Strategy

Methodology: Divide & Conquer.

From a project point of view, we divide the entire project into several layers, with the top layer being the architectural design layer, followed by the business logic layer, then various dependency libraries and infrastructure, and at the bottom, there are various atomic components (for example random number generators, language features).

We can show a ZKP application from the perspective of security audit (see Fig.1).

Fig.1. The ZKP application from the perspective of security audit

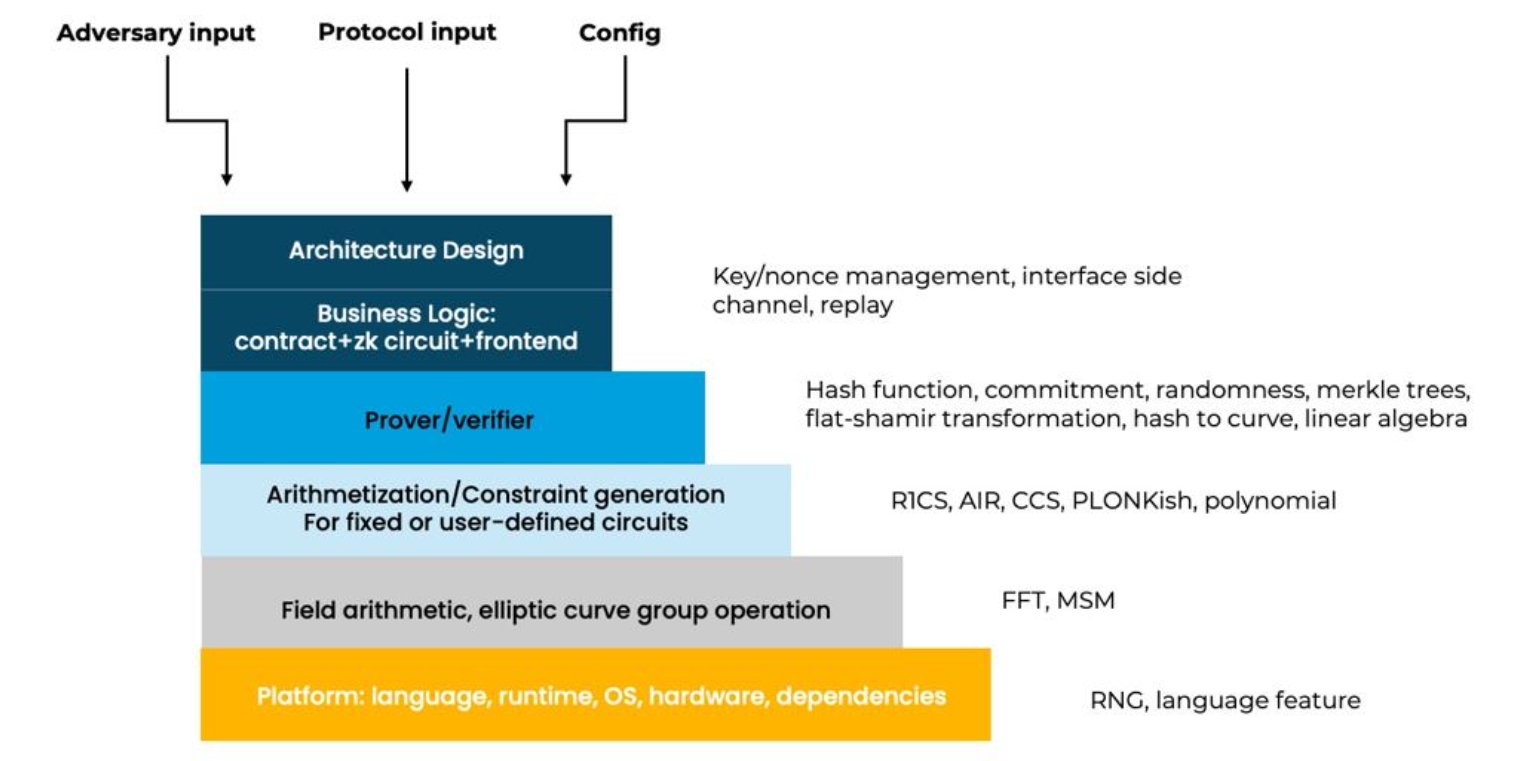
• At the topmost layer is the Application Layer, which comprises two main components: high-level architectural design and business logic, including contracts, circuits, and front-end. This layer must deal with potential malicious user inputs, protocol inputs, and configuration settings. Ensuring the security of key/nonce management and interfaces, while guarding against sidechannel attacks and replay attacks, is crucial.

• Secondly, the Prover/Verifier Layer aims to fulfill the roles of the two parties involved in the zero-knowledge protocol. For this, it is necessary to implement and protect various cryptographic primitives that support the circuit and proof system. These include but are not limited to hash function, commitment, randomness, merkle trees, fiat-shamir transformation, hash-to-curve, and linear algebra.

• The next layer down is designed to support the two roles above, requiring more foundational operations, such as circuit arithmetization and constraint generation. Typical arithmetization strategies include R1CS, AIR, CCS, and PLONKish, along with their necessary polynomial implementations.

• The layer below involves field arithmetic and elliptic curves groups operations. Acceleration algorithms for these operations, such as FFT and MultiScalar Multiplication (MSM), can be considered.

• The foundational layer pertains to platform-specific elements: programming language, runtime, OS, hardware, and dependencies. Consideration must be given to the characteristics (and flaws) of the programming language itself, RNG, and other factors.

This layered approach enables a comprehensive and secure implementation of ZKP protocols, ensuring that each layer builds upon the secure foundation of the layer below it, from managing application-specific logic and security issues to efficiently utilizing underlying hardware and software platforms.

The audit team should conduct threat modeling before beginning the audit. Threat modeling involves creating a list of potential vulnerabilities for each layer of the project, thereby allowing them to address every possible error. Moreover, it is advisable for each member of the audit team to perform a line-by-line code inspection, followed by an internal cross-review. These measures ensure that the entire ZKP audit can not only identify vulnerabilities within ZK circuits but also highlight design flaws in the ZKP application and pinpoint any inaccuracies in the integration process of ZK primitives.

4.3 The Role of Audit Tools in Circuit Auditing

To facilitate the auditing of ZKP applications, the industry has developed a variety of audit tools. These tools are primarily static analyzers[33], designed to identify common vulnerabilities within ZKP circuits. Depending on the static analysis method adopted, these tools can be classified into two main categories: abstract interpretation and formal verification. Abstract interpretation methods use abstract domains to approximate the representation of values in concrete domains and approximate concrete functions and transformations, thus detecting vulnerabilities in zero-knowledge circuits. Formal verification tools, on the other hand, use mathematical logic and methods to prove the correctness and security of systems. This method provides rigorous and trustworthy proofs, effectively avoiding human errors and vulnerabilities[34–36].

For example, audit tools such as Ecne and Circomspect[37] employ abstract interpretation methods, while tools like Veridise’s Coda[38] use formal verification methods. Others, like korrekt and Picus, combine these two approaches. They first conduct a preliminary vulnerability screening using abstract interpretation methods, followed by an in-depth security inspection using formal verification methods to ensure the security of the ZKP circuit. However, these tools can only provide limited assistance, auditors should not rely solely on these tools to perform circuit audits[39].

5 Conclusion

This article has embarked on a comprehensive exploration of the vulnerabilities inherent in Zero-Knowledge Proof (ZKP) technologies, underpinning the crucial balance between maintaining stringent security protocols and fostering the revolutionary potential of ZKPs in enhancing privacy and completeness within blockchain and other cryptographic systems. Through meticulous classification and analysis of various vulnerabilities, ranging from completeness and soundness issues to information leakage and non-standardized cryptographic implementations, we have delineated the intricate challenges posed by the complex implementation and rapid iteration inherent in ZKP technologies.

The vulnerabilities and defense mechanisms discussed herein underscore a broader discourse on the necessity of continuous vigilance, innovation, and refinement in the security auditing of cryptographic systems. As ZKP technologies evolve and their applications become increasingly integral to the cryptographic infrastructure, the challenges of ensuring their security and reliability become more complex and demanding.

Looking forward, the field of ZKP and its security auditing beckons for further research and development. This entails not only the enhancement of existing audit tools and methodologies but also a collaborative effort among researchers, developers, and practitioners to forge novel solutions that address the ever-evolving landscape of vulnerabilities. Such endeavors will be pivotal in harnessing the full potential of ZKP technologies, paving the way for a more secure, private, and efficient cryptographic future.

References

1. Lipmaa, Helger, Roberto Parisella, and Janno Siim. "Constant-Size zk-SNARKs in ROM from Falsifiable Assumptions." Cryptology ePrint Archive (2024).
2. Liu, Xuanming, Zhelei Zhou, Yinghao Wang, Bingsheng Zhang, and Xiaohu Yang. "Scalable Collaborative zk-SNARK: Fully Distributed Proof Generation and Malicious Security." Cryptology ePrint Archive (2024).
3. Bellés-Muñoz, Marta, Miguel Isabel, Jose Luis Muñoz-Tapia, Albert Rubio, and Jordi Baylina. "Circom: A circuit description language for building zero-knowledge applications." IEEE Transactions on Dependable and Secure Computing (2022).
4. Chiesa, Alessandro, Yuncong Hu, Mary Maller, Pratyush Mishra, Noah Vesely, and Nicholas Ward. "Marlin: Preprocessing zkSNARKs with universal and updatable SRS." In Advances in Cryptology–EUROCRYPT 2020: 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, May 10–14, 2020, Proceedings, Part I 39, pp. 738-768. Springer International Publishing, 2020.
5. Weng, Chenkai, Kang Yang, Jonathan Katz, and Xiao Wang. "Wolverine: fast, scalable, and communication-efficient zero-knowledge proofs for boolean and arithmetic circuits." In 2021 IEEE Symposium on Security and Privacy (SP), pp. 1074-1091. IEEE, 2021.
6. Baum, Carsten, Alex J. Malozemoff, Marc B. Rosen, and Peter Scholl. "Mac’n’Cheese: Zero-Knowledge Proofs for Boolean and Arithmetic Circuits with Nested Disjunctions." In Advances in Cryptology–CRYPTO 2021: 41st Annual International Cryptology Conference, CRYPTO 2021, Virtual Event, August 16–20, 2021, Proceedings, Part IV 41, pp. 92-122. Springer International Publishing, 2021.
7. Xie, Tiacheng, Jiaheng Zhang, Yupeng Zhang, Charalampos Papamanthou, and Dawn Song. "Libra: Succinct zero-knowledge proofs with optimal prover computation." In Advances in Cryptology–CRYPTO 2019: 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 18–22, 2019, Proceedings, Part III 39, pp. 733-764. Springer International Publishing, 2019.
8. Baum, Carsten, Robin Jadoul, Emmanuela Orsini, Peter Scholl, and Nigel P. Smart. "Feta: efficient threshold designated-verifier zero-knowledge proofs." In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, pp. 293-306. 2022.
9. Giacomelli, Irene, Jesper Madsen, and Claudio Orlandi. "ZKBoo: Faster ZeroKnowledge for Boolean Circuits." In 25th usenix security symposium (usenix security 16), pp. 1069-1083. 2016.
10. Ernstberger, Jens, Stefanos Chaliasos, Liyi Zhou, Philipp Jovanovic, and Arthur Gervais. "Do You Need a Zero Knowledge Proof?" Cryptology ePrint Archive(2024).
11. Luong, Duc Anh, and Jong Hwan Park. "Privacy-preserving identity management system on blockchain using Zk-SNARK." IEEE Access 11 (2023): 1840-1853.
12. Rathee, Deevashwer, Guru Vamsi Policharla, Tiancheng Xie, Ryan Cottone, and Dawn Song. "ZEBRA: SNARK-based Anonymous Credentials for Practical, Private and Accountable On-chain Access Control." Cryptology ePrint Archive (2022).
13. Wan, Zhiguo, Yan Zhou, and Kui Ren. "zk-AuthFeed: Protecting data feed to smart contracts with authenticated zero knowledge proof." IEEE Transactions on Dependable and Secure Computing 20, no. 2 (2022): 1335-1347.
14. Gabizon, A. "On the Security of the BCTV Pinocchio zk-SNARK Variant." Cryptologv ePrint Archive. Paper 2019/119, 2019. 9p.
15. Chaliasos, Stefanos, Jens Ernstberger, David Theodore, David Wong, Mohammad Jahanara, and Benjamin Livshits. "SoK: What don’t we know? Understanding Security Vulnerabilities in SNARKs." arXiv preprint arXiv:2402.15293 (2024).
16. Dao, Quang, Jim Miller, Opal Wright, and Paul Grubbs. "Weak fiat-shamir attacks on modern proof systems." In 2023 IEEE Symposium on Security and Privacy (SP), pp. 199-216. IEEE, 2023.
17. Garg, Sanjam, Aarushi Goel, Abhishek Jain, Guru-Vamsi Policharla, and Sruthi Sekar. "zkSaaS: Zero-Knowledge SNARKs as a Service." In 32nd USENIX Security Symposium (USENIX Security 23), pp. 4427-4444. 2023.
18. Quan, Yunjia. "Enhancing Ethereum’s Security with LUMEN, a Novel ZeroKnowledge Protocol Generating Transparent and Efficient zk-SNARKs." arXiv preprint arXiv:2312.14159 (2023).
19. Bowe, Sean, Ariel Gabizon, and Matthew D. Green. "A multi-party protocol for constructing the public parameters of the Pinocchio zk-SNARK." In Financial Cryptography and Data Security: FC 2018 International Workshops, BITCOIN, VOTING, and WTSC, Nieuwpoort, Curaçao, March 2, 2018, Revised Selected Papers 22, pp. 64-77. Springer Berlin Heidelberg, 2019.
20. Ben-Sasson, Eli, Alessandro Chiesa, Matthew Green, Eran Tromer, and Madars Virza. "Secure sampling of public parameters for succinct zero knowledge proofs." In 2015 IEEE Symposium on Security and Privacy, pp. 287-304. IEEE, 2015.
21. Garoffolo, Alberto, Dmytro Kaidalov, and Roman Oliynykov. "Snarktor: A Decentralized Protocol for Scaling SNARKs Verification in Blockchains." Cryptology ePrint Archive (2024).
22. Soler, David, Carlos Dafonte, Manuel Fernández-Veiga, Ana Fernández Vilas, and Francisco J. Nóvoa. "A Privacy-preserving key transmission protocol to distribute QRNG keys using zk-SNARKs." Computer Networks (2024): 110259.
23. kcharbo3, and Mirror-Tang, et al. "ZK Bug Tracker.". https://zenodo.org/doi/10.5281/zenodo.10851249.
24. ChainLight. “Patch Thursday — Uncovering a ZK-EVM Soundness Bug in zkSync Era.” 2023. https://medium.com/chainlight/uncovering-a-zk-evm-soundness-bugin-zksync-era-f3bc1b2a66d8.
25. Kyle Charbonnet, and Yuefei Li. "MACI Security Audit." 2024. https://maci.pse.dev/assets/files/20240223_PSE_Audit_audit_reporta181b98b05198c102be49113c354b5f2.pdf
26. Ben-Sasson, Eli, Iddo Bentov, Yinon Horesh, and Michael Riabzev. "Scalable zero knowledge with no trusted setup." In Advances in Cryptology–CRYPTO 2019: 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 18–22, 2019, Proceedings, Part III 39, pp. 701-732. Springer International Publishing, 2019.
27. Setty, Srinath. "Spartan: Efficient and general-purpose zkSNARKs without trusted setup." In Annual International Cryptology Conference, pp. 704-737. Cham: Springer International Publishing, 2020.
28. Wahby, Riad S., Ioanna Tzialla, Abhi Shelat, Justin Thaler, and Michael Walfish. "Doubly-efficient zkSNARKs without trusted setup." In 2018 IEEE Symposium on Security and Privacy (SP), pp. 926-943. IEEE, 2018.
29. He, Daojing, Zhi Deng, Yuxing Zhang, Sammy Chan, Yao Cheng, and Nadra Guizani. "Smart contract vulnerability analysis and security audit." IEEE Network 34, no. 5 (2020): 276-282.
30. Park, Chansol, Janghwan Kim, and R. Young Chul Kim. "Smart Contract Security Audit Trends and Services." The Journal of the Convergence on Culture Technology 9, no. 6 (2023): 1017-1029.
31. Doelitzscher, Frank. "Security audit compliance for cloud computing." PhD diss., Plymouth University, 2014.
32. Pereira, Teresa, and Henrique Santos. "A security audit framework to manage Information system security." In Global Security, Safety, and Sustainability: 6th International Conference, ICGS3 2010, Braga, Portugal, September 1-3, 2010. Proceedings 6, pp. 9-18. Springer Berlin Heidelberg, 2010.
33. Wen, Hongbo, Jon Stephens, Yanju Chen, Kostas Ferles, Shankara Pailoor, Kyle Charbonnet, Isil Dillig, and Yu Feng. "Practical Security Analysis of ZeroKnowledge Proof Circuits." IACR Cryptol. ePrint Arch. 2023 (2023): 190.
34. Coglio, Alessandro, Eric McCarthy, and Eric W. Smith. "Formal verification of zero-knowledge circuits." arXiv preprint arXiv:2311.08858 (2023).
35. Coglio, Alessandro, Eric McCarthy, Eric Smith, Collin Chin, Pranav Gaddamadugu, and Michel Dellepere. "Compositional formal verification of zeroknowledge circuits." Cryptology ePrint Archive (2023).
36. M. Isabel, C. Rodríguez-Núñez and A. Rubio, "Scalable Verification of ZeroKnowledge Protocols," in 2024 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 2024 pp. 132-132.
37. Pailoor, Shankara, Yanju Chen, Franklyn Wang, Clara Rodríguez, Jacob Van Geffen, Jason Morton, Michael Chu, Brian Gu, Yu Feng, and Işıl Dillig. "Automated detection of under-constrained circuits in zero-knowledge proofs." Proceedings of the ACM on Programming Languages 7, no. PLDI (2023): 1510-1532.
38. Liu, Junrui, Ian Kretz, Hanzhi Liu, Bryan Tan, Jonathan Wang, Yi Sun, Luke Pearson, Anders Miltner, Işıl Dillig, and Yu Feng. "Certifying zero-knowledge circuits with refinement types." arXiv preprint arXiv:2304.07648 (2023).
39. Stodt, Jan, Daniel Schönle, Christoph Reich, Fatemeh Ghovanlooy Ghajar, Dominik Welte, and Axel Sikora. "Security audit of a blockchain-based industrial application platform." Algorithms 14, no. 4 (2021): 121.